先週の金曜日の夕方、久しぶりに国会前に足を延ばしてみた。この寒い中、みんな、よくがんばっている!感動した。
しかし、昨年の夏と比べると明らかに人数は減っている。「反対の大合唱」というよりは、拡声器が一人叫んでいる感じ。とはいえ、事故当初から比べれば、相当な人数が、国会や官邸、そして経産省の前を歩きながら「国民の意見」を示している。彼らは永田町や霞ヶ関の歩道を静かに歩きながらも、「国策」の失敗を追及し、国に深く反省するよう督促している。これが民主主義の基本というものだろう。それは古くて、新しい(少なくとも今の日本においては)。
広渡先生の著書「学者にできることは何か」を買った。前の日本学術会議の会長を努めた人だ。法学者(京都大学法学部出身)。実は、自然科学以外の学者が学術会議の会長になったのは彼が初めて。東大名誉教授、元東大副学長、民主主義科学者協議会法律部会理事長、などの肩書きが巻末に書かれている。が、権威に寄りかかり、「寅の威を借る狐」のような学者たちとは一線を画している。
それがよくわかるのが、大震災の後、変貌した日本社会に対し、「極度の緊張感から、体調を崩した」と書かれている本の冒頭だ。スーパーやレストランで、セシウム137やヨウ素131などの放射能物質に汚染された食物を避けようと、必死に産地について問い合わせをする人たち(その多くは「母親」たちだろう)を、「気にし過ぎ」、「非科学的で、無知の表れ」などと卑下し、馬鹿にする人たちは、広渡氏の体調不良も笑い飛ばし、馬鹿にするだけの覚悟を持たねばなるまい。
広渡清吾著
「学者にできることは何か:日本学術会議のとりくみを通して」
岩波書店(2012年)震災と社会シリーズ第7巻
2013年2月20日水曜日
やぶそばが焼けてしまった...
「いちまあーーーいーー」と相撲の呼び出しのような、そうでないような独特の注文の取り方に度肝を抜かれ、また一枚のザルの少なさに度肝を抜かれ、そして江戸情緒の残る素晴らしい雰囲気に驚かされたのが、神田にあった「やぶそば」(というより、ほぼ秋葉原)。「たけむら」と合わせ、秋葉原の買い物の後、よく立ち寄ったものだ。日本に帰国してから、今度行こう今度行こうとずるずる延ばしていたのがよくなかった...かなりの常連客がついていると思うので、必ず再建してくれると思う。
2013年2月17日日曜日
東大の2次試験の数学:2003年の第6問
東大の2次試験の問題を見ていったら、2003年の第6問に出くわした。思わず笑ってしまった。それは、「円周率が3.05より大きいことを証明せよ。」たったこれだけ。ヒントはなし。しかし、これはすごくいい問題だと思った。とにかく、「よく考える」必要がある。
とはいえ、限られた時間内に、この問題に取り組めるだけの精神的余裕があるかどうかは別の話となろう。この問題を見て、パニック状態に陥った学生はかなりいたはずだ。とはいえ、こういう問題に取り組んでこそ、「本当の勉強(ある意味、研究かも)」だ。しかし、いったん方針が立てば、これほど簡単な問題もない。中学生でも解けるだろう。その意味は、おいおい明らかになろう。私がこの問題を見て、どのように思考していったか、記述してみる。
最初は3.05の意味を考えてみた。3と5/100、つまり3+(1/20)。1/20? なにか意味のある数字なのか?しばらく粘ってみたが、思いつかないので、この線で解くのはあきらめる。(5分くらい?)
次に思いついたのは、arctan(1)=π/4を利用して、左辺をテイラー展開して、不等式で押さえ込んでいくというもの。しかし、arctan(x)のテイラー展開の符号は交代的になるので、不等式で下限を抑えにくい。さらに、テイラー展開は高校の数学では教えない。よって、この線もあきらめる。(ここまで10分程度。)
ということで、やっぱり図形的に考える事にする。円周率のそもそもの意味は、円周の長さに対する直径の比率、ということだから、半径1の円の円周の長さを簡単な図形で近似して、それが円周より短くなればいいはずだ。つまり、円周/直径=πだから、「ある簡単な図形の周長」÷ 直径(半径が1だとすると2)が、うまい具合に3.05程度になる図形がどこかに出てくるはず、と当たりをつける。まあ、最初は円に内接する正三角形か、正方形から始めるべきだろう。なんといっても、小学校から馴染みのある図形である。(正多角形(n角形)が便利なのは、一辺の長ささえ計算すれば、あとはそれをn倍するだけで、その図形の周長が求まるから。)
三角形より四角形の方が、より「厳しい」近似なのは確かだから、まずは正方形から計算を始める事にする(左図に相当)。
正方形をさらに4つに分割し、2等辺直角三角形の「斜辺」、つまり一番長い辺の長さを計算する。半径が1なので、簡単に√2ということが求まる。これが4つあるから、4√2が正方形の周長となる。これを円の直径2で割ったものが、円周率に対する近似となるが、内接しているので明らかにπよりは小さくなるはず。すなわち、π>2√2という不等式が得られた。右辺が見事に3.05となっていれば、ここで証明は終わりになるのだが、さすがにこれは東大の入学試験問題だ。そうは問屋が下ろさないはず。√2=1.4142くらいは理系人間でなくとも覚えているはず。これを代入すると、π>2.8284となった。残念!3.05よりはずっと小さい。つまり、正方形では近似が粗すぎるのだ。(ここまで15分。)
とはいえ、限られた時間内に、この問題に取り組めるだけの精神的余裕があるかどうかは別の話となろう。この問題を見て、パニック状態に陥った学生はかなりいたはずだ。とはいえ、こういう問題に取り組んでこそ、「本当の勉強(ある意味、研究かも)」だ。しかし、いったん方針が立てば、これほど簡単な問題もない。中学生でも解けるだろう。その意味は、おいおい明らかになろう。私がこの問題を見て、どのように思考していったか、記述してみる。
最初は3.05の意味を考えてみた。3と5/100、つまり3+(1/20)。1/20? なにか意味のある数字なのか?しばらく粘ってみたが、思いつかないので、この線で解くのはあきらめる。(5分くらい?)
次に思いついたのは、arctan(1)=π/4を利用して、左辺をテイラー展開して、不等式で押さえ込んでいくというもの。しかし、arctan(x)のテイラー展開の符号は交代的になるので、不等式で下限を抑えにくい。さらに、テイラー展開は高校の数学では教えない。よって、この線もあきらめる。(ここまで10分程度。)
ということで、やっぱり図形的に考える事にする。円周率のそもそもの意味は、円周の長さに対する直径の比率、ということだから、半径1の円の円周の長さを簡単な図形で近似して、それが円周より短くなればいいはずだ。つまり、円周/直径=πだから、「ある簡単な図形の周長」÷ 直径(半径が1だとすると2)が、うまい具合に3.05程度になる図形がどこかに出てくるはず、と当たりをつける。まあ、最初は円に内接する正三角形か、正方形から始めるべきだろう。なんといっても、小学校から馴染みのある図形である。(正多角形(n角形)が便利なのは、一辺の長ささえ計算すれば、あとはそれをn倍するだけで、その図形の周長が求まるから。)
三角形より四角形の方が、より「厳しい」近似なのは確かだから、まずは正方形から計算を始める事にする(左図に相当)。
 |
| postscriptで図形を描いてみた。 (高校数学ではpostscriptをどんどん教えるべきではないだろうか?) |
そこで、今度は正8角形にチャレンジする(上の右図)。基本的な図形を抜き出して考える(下図)。
円の半径が1であるということ、正方形の拡張になっていること(例えば、角AOB=90度であることや、AB=√2であることなど)、などを元に考えれば、中学生程度の知識でも(つまりはピタゴラスの定理)、CB2= (1/2) + (1-1/√2)2であることは計算できる。これを8倍すると、正八面体の周長となる。
円周率の近似はそれを2で割った数になるから、
となる。電卓でこの数字を計算してみると、3.0614676....となる。これは3.05より大きい数だから、見事にπ>3.05が証明できたことになる。しかし、日本の大学では、試験会場に電卓を持ち込む事ができない。果たして、√2の値をどこまで覚えていたら、このやり方で解けるのだろうか?
まず、√2 〜1.414で試してみる。2-1.414 = 0.5858となる。こいつの平方根を計算するのは大変なので、まずは近似的に見て見よう。0.72=0.49であり、0.82=0.64だから、明らかに0.5858の平方根は0.7と0.8の間にある。中点の0.75で試してみよう。0.75×0.75 = 0.5625となる。結構いい値が出た。しかし、この値を4倍すると2.25にしかならない。3.05とはほど遠い。(試験会場でこの結果が出たら、心の弱い学生はここであきらめてしまうかもしれない。)では、0.76はどうだろうか?0.762=0.5776。0.5858にさらに近づいた。4×0.5776=2.3104...だめだ。全然届かない。0.77はどうか?0.772=0.5929>0.5858。これはオーバーしてしまうので、採用できない。
ということは、0.76と0.77の間の数を狙わなければならない、ということになる。精度を一つ上げて、0.765で試してみよう。0.7652=0.585225! オーッ!かなり近い値が出た。これならいけるのでは?! 0.765 × 4 = 3.06 (>3.05)!!!やったー!
これで証明終わり、となる。近似計算で少数第3位まで、心が折れずにもっていけるかどうかが、この方法での勝負の分かれ目となる。実際、最後の試行錯誤に時間がかかり、全部で30〜40分程度の時間がかかってしまった。しかし、計算の中身は、簡単な中学レベルの幾何、それから平方根の(簡単な)数値解析だけだ。もちろん、電卓があったら数値解析は不要になる。つまり、この問題は中学生でも解ける問題なのだ。
火星探検のメンバーの一人に選ばれたあなたは、火星の周回軌道上で事故に遭遇。その影響で、コンピュータ、電卓、通信機器などすべてのエレクトロニクスデバイスが故障してしまった。地球まで帰還するために、ロケットの噴射時間を手で計算することになったあなたは、その計算の最後の最後に、円周率の値が必要になったのである。義務教育で、π〜3と教わっていたあなたは、それをもとに軌道計算をしたが、一抹の不安を感じる。「ほんとうにこんな整数近似で地球にちゃんと帰還できるのだろうか?」と。幸い、πの値は3より大きいことは覚えていたあなたは、円周率を3+εと変数表示し分析してみた。するとπを3.05より大きく見積もった場合と、3.05より小さく見積もった場合で噴射時間は大きく2つに分かれることがわかった。そこで、多角形近似を用いて、円周率のより精度の高い近似を求めることを思いつく。ロケット噴射までのタイムリミットはあと30分。それを超えてしまうと、永遠に地球に戻ることは不可能となる。あまり多くの正多角形のケースを試す事はできない。はたしてあなたは、π>3.05を証明し、地球に帰還することはできただろうか?このとき、あなたの運命を決めるのは、少数第三位までの近似なのである!
まず、√2 〜1.414で試してみる。2-1.414 = 0.5858となる。こいつの平方根を計算するのは大変なので、まずは近似的に見て見よう。0.72=0.49であり、0.82=0.64だから、明らかに0.5858の平方根は0.7と0.8の間にある。中点の0.75で試してみよう。0.75×0.75 = 0.5625となる。結構いい値が出た。しかし、この値を4倍すると2.25にしかならない。3.05とはほど遠い。(試験会場でこの結果が出たら、心の弱い学生はここであきらめてしまうかもしれない。)では、0.76はどうだろうか?0.762=0.5776。0.5858にさらに近づいた。4×0.5776=2.3104...だめだ。全然届かない。0.77はどうか?0.772=0.5929>0.5858。これはオーバーしてしまうので、採用できない。
ということは、0.76と0.77の間の数を狙わなければならない、ということになる。精度を一つ上げて、0.765で試してみよう。0.7652=0.585225! オーッ!かなり近い値が出た。これならいけるのでは?! 0.765 × 4 = 3.06 (>3.05)!!!やったー!
火星探検のメンバーの一人に選ばれたあなたは、火星の周回軌道上で事故に遭遇。その影響で、コンピュータ、電卓、通信機器などすべてのエレクトロニクスデバイスが故障してしまった。地球まで帰還するために、ロケットの噴射時間を手で計算することになったあなたは、その計算の最後の最後に、円周率の値が必要になったのである。義務教育で、π〜3と教わっていたあなたは、それをもとに軌道計算をしたが、一抹の不安を感じる。「ほんとうにこんな整数近似で地球にちゃんと帰還できるのだろうか?」と。幸い、πの値は3より大きいことは覚えていたあなたは、円周率を3+εと変数表示し分析してみた。するとπを3.05より大きく見積もった場合と、3.05より小さく見積もった場合で噴射時間は大きく2つに分かれることがわかった。そこで、多角形近似を用いて、円周率のより精度の高い近似を求めることを思いつく。ロケット噴射までのタイムリミットはあと30分。それを超えてしまうと、永遠に地球に戻ることは不可能となる。あまり多くの正多角形のケースを試す事はできない。はたしてあなたは、π>3.05を証明し、地球に帰還することはできただろうか?このとき、あなたの運命を決めるのは、少数第三位までの近似なのである!
2013年2月13日水曜日
福島の子供の甲状腺癌:さらに2人
昨年の9月に、福島原発事故以後、最初の「こどもの甲状腺癌」が報告された(福島県は原発の因果関係を否定しているが)。
そして、今日新たに二人の子供(追記:年齢は15歳くらいだとか)の甲状腺癌が報告された。加えて、朝日新聞によれば、7人が甲状腺癌の疑いが濃いという結果が出たという。(追記:これまでの患者計10人の内、男3人女7人の比率だという。)
甲状腺癌は大人の病気であり、子供がかかるとしたら相当稀なケースなはずだ。それが、人口200万人足らずの福島県において、この半年で3人〜10人が甲状腺癌になったというのは、ちょっと確率からして高すぎるように感じる。
そもそも、その他の県ではどのくらいの割合でこどもの甲状腺癌が発症しているのだろうか?そういう統計をすぐに自治体、政府は発表すべきだろう。他の自治体と比べて、発症率が同じ程度なら「原発事故とは無関係とみられる」と言ったっていい。ところが、「原発由来の甲状腺癌は、事故から4、5年後にならないと発症しない。だから今回のケースは原発と関係ない。」という説明は、科学的に見えて、実は非科学的な匂いがある。
今回手術を受ける事になった子供達の手術費は、絶対に東電と政府が払うべきだ。「原発事故と関係ない」などといって責任逃れをしようとしたら、厳しく糾弾しなくてはならないと思う。そもそも、東電は国会の調査に対しても嘘をついたことが判明しているわけだから、私たちは根拠の無い楽観的な「説明」には注意しないといけない。
そして、今日新たに二人の子供(追記:年齢は15歳くらいだとか)の甲状腺癌が報告された。加えて、朝日新聞によれば、7人が甲状腺癌の疑いが濃いという結果が出たという。(追記:これまでの患者計10人の内、男3人女7人の比率だという。)
甲状腺癌は大人の病気であり、子供がかかるとしたら相当稀なケースなはずだ。それが、人口200万人足らずの福島県において、この半年で3人〜10人が甲状腺癌になったというのは、ちょっと確率からして高すぎるように感じる。
そもそも、その他の県ではどのくらいの割合でこどもの甲状腺癌が発症しているのだろうか?そういう統計をすぐに自治体、政府は発表すべきだろう。他の自治体と比べて、発症率が同じ程度なら「原発事故とは無関係とみられる」と言ったっていい。ところが、「原発由来の甲状腺癌は、事故から4、5年後にならないと発症しない。だから今回のケースは原発と関係ない。」という説明は、科学的に見えて、実は非科学的な匂いがある。
今回手術を受ける事になった子供達の手術費は、絶対に東電と政府が払うべきだ。「原発事故と関係ない」などといって責任逃れをしようとしたら、厳しく糾弾しなくてはならないと思う。そもそも、東電は国会の調査に対しても嘘をついたことが判明しているわけだから、私たちは根拠の無い楽観的な「説明」には注意しないといけない。
2013年2月9日土曜日
2013年2月7日木曜日
東大の二次試験の数学:2012年の場合
今年のセンター試験の数学IAは第3問が難しかったと思う。実は中学でならった幾何の定理を幾つか利用しないと短時間で解く事が難しい。全てを高校の授業で習ったように代数的に解こうとすると足をすくわれる。計算量が多くなって、「爆発」してしまうのだ。これだと、「センター試験というのは中学の勉強の習熟度を試す試験なのだろうか?」という疑問も生じかねない。一応、三角関数は出てくるが、この問題で一番よく使うのはピタゴラスの定理(三平方の定理)ではないだろうか?直角の場所を探して、後はa2+b2=c2を適用。これってまさに中学の問題だ。もちろん、高校数学の要素も散りばめられてはいたが....
この問題を思えば、昨年の東大の2次試験の数学の方がずっと簡単で、よい問題が含まれていたと思う(全部は見てないので断定はできないが)。例えば、第5問の平行四辺形と一次変換を組み合わせた問題は、大学に入ってから再登場する概念が組み合わされていて、後でとても役に立つと思われる。だから、答えを得るだけではなく、その内容の吟味が大事だろう。もちろん、試験中の学生は正解を得ることだけを考えればよいのだが、日頃の勉強では存分に問題を研究し、その真の意味や背景をえぐり出すよう努力すべきだ。
ちなみに、東大の理系の数学は150分で6問を解く。全問解答を狙うなら、一つ25分ということになるが、昨年の第5問はちょうどそのくらいの時間で解ける。(よく訓練された受験生ならもっと短い時間で解けるだろう。)
さて、この問題から学べることを探してみる。2次元の正方行列。行列要素はすべて整数。たぶん、この「整数」というのが強い条件になるはず。量子力学でも整数は大きな役割を果たす。実数と違って、整数には「隙間」があるからだ。最後に、この行列要素から作ったベクトルがなす平行四辺形の面積は1になるという。実際に問題を解くときは、この条件をどう使うかが問題となろう。
2つのベクトルが成す平行四辺形の面積は、大学では電磁気学でよく取り上げられる。今思いつくのはポインティングベクトル。これは、電磁場によって運ばれるエネルギー流(束)のことで、イメージとしては太陽からやってくるエネルギー、いわゆる「太陽エネルギー」がよい例となろう。youtubeに公開されているMIT物理の講義の一つがまさにポインティングベクトルについてであり、実は太陽エネルギーの例もこの講義の中で取り上げられている。
ポインティングベクトル(S)は、電場ベクトル(E)と磁場ベクトル(B)の外積で表される、つまりS=E×B(比例定数は1に規格化した....)。このエネルギー流の大きさ(たとえば太陽エネルギーの大きさ)を計算するときは、Sの大きさ(ノルム)を計算することになるが、それがまさにEとBがつくる「平行四辺形の面積」の計算に相当している。
電場と磁場の2つのベクトルの外積の結果得られたベクトル(すなわちS)の方向は、この平行四辺形がつくる面に垂直な方向を向いている。このことから、電磁場というのは横波であり、電磁場の揺れる方向に対して垂直方向に電磁波自体は伝搬するという性質がわかる。
ベクトルEとベクトルBの成す角度をθとすると、ベクトルSの大きさ(ノルム)は|S|=|E×B| = |E| |B| sinθで与えられる。これはベクトル成分を書き下して確かめてみてもいいし、いろいろな方法で確認できるだろう。実は、2つのベクトルの外積のノルムは、そのベクトルが成す平行四辺形の面積になっていることは、図に描いて結果を分析すれば明らかとなる。上手に座標系を選んで(実はこの「上手に座標系を選んで」というのが物理では非常に大事な考え方だ。これが出来る人が物理が出来る人、と言い換えてもいいくらい)、電場Eが底辺となるようにする。当然、平行四辺形の底辺の長さは|E|で与えられる。一方、平行四辺形の高さは|B|sinθとなる。平行四辺形の面積は、底辺×高さだから、|E||B|sinθとなる。これは外積のノルム|E×B|、すなわちポインティングベクトルの大きさ|S|に等しい。
回転操作を座標全体に対して行えば(つまり座標軸の回転変換)、特別な状況から一般的な状況にもどることができる。ここで大切なのは、回転操作はベクトル同士が成す角度を不変に保つという性質だ。また、ノルム(つまりベクトルの長さ)も回転操作に対して不変だというのも大事だ。このように、ある座標変換に対して「不変な量」を探し出すのが、量子力学が誕生して以降の物理学の考え方の基本だ。この問題でも、それに似たようなことを「楽しむ」ことはできる。すなわち、x軸を電場に沿って取った特別な座標から、電場が(a,b)、磁場が(c,d)を向いているような一般座標に回転変換したとしよう。この変換をしても角度θとノルム|E|と|B|は不変なんだから、平行四辺形の面積も不変に保たれる(当然といえば当然だが)。この座標において、|E|と|B|は、それぞれ(a,b)と(c,d)を使って表される(ピタゴラスの定理)。また、θに関してはEとBの内積E・Bによって表す事ができる(正確にはcosθの形だが...)。sin2θ+cos2θ=1を使えば、sineとcosの変換は自由にできるから、内積とノルムを使って、どんな座標系でも使える平行四辺形の面積公式を得る事ができる。内積の定義からE・B=|E||B|cosθ。これをsinθに変換し、上で求めた平行四辺形の面積公式、つまりS=|E||B|sinθに代入すると、
を得る。なかなか綺麗な公式だ!この形は座標の選び方によらないユニバーサルな表式になっている。そこで、回転変換して一般的な状況にした後のE、Bのベクトル成分を使ってSを書き直すと、S=|ad-bc|という形になる。これはこれできれいな形だし、また問題で与えられた行列Aの行列式(determinant,またはdet)にも一致している。きっと、出題した先生は、平行四辺形の面積と2次元正方行列のdetが同じ形をしている、という偶然をうまく利用したかったのだろう。(両者が反対称性をもつことを知れば、この偶然はそれほど偶然というわけではないだろうが。)
題意から、四辺形の面積は1に拘束されているのでS=1であるが、ad-bc=det(A)、つまりAの行列式の値としてはdet(A)=±1ということになる。実はこのようなタイプの行列をユニタリー行列といって、量子力学で最も重要な変換行列として頻繁に登場する。ちなみに、det(A)=1は回転などパリティが変わらないタイプの変換に相当し、det(A)=-1は鏡映反転などパリティが変わるタイプの変換に相当する。同じユニタリー変換といっても、det(A)の符号が異なる変換同士は連続変換によって結びつけることはできない。ちなみに、行列Bのdetは1だから(det(B)=1)、ある種の回転操作と見なすことができる。
(1)では、とりあえず行列の計算はやってみてもよいだろうが、基本的には行列式を中心に考えるのがよい。detの関係式として有名なものに、det(A)det(B)=det(AB) = det(BA)というのがある。この問いではまさにこれを使う。det(B)=1であることはすでに考察済みだから、det(BA)=det(A)となる。|det(A)|=|ad-bc|=1だから、行列BAの行列要素でつくる平行四辺形の面積は、行列Aの要素でつくる平行四辺形の面積と同じ1であることが示された。
同じようにして、B-1B=E、Eは単位行列、に関して行列式を考えると、det(B-1)det(B) = det(E)、Eは単位行列、なので、det(B-1)= 1/ det(B)=1を得る。従って、det(B-1A)=det(A)=±1となり、この行列要素からなる平行四辺形も面積が1のままであることがわかる。
BAやB-1Aの行列要素が整数のままであるのは、行列の積は、行列要素の観点からすると、和と積の2種類の演算の組み合わせ(つまり線形結合)だから、この演算は閉じている(つまり計算の結果が、整数の集合から飛び出さない)ことがわかる。和と積という2種類の演算が定義された集合の事を「環」、あるいは「代数系」というらしい。仮に、行列の積に割算が含まれるようなことになると、整数÷整数は必ずしも整数に戻らないから、演算は閉じず、結果の行列が非整数の行列要素をもってしまうこともあり得る。行列の積は「線形結合」なんですよ!という出題者からのメッセージだと、この問題は受け取るべきだろう。実際、大学に入学して、最初に理系の学生が挫折しかかり、ショックを受けるのが、線形代数の「一次独立」、「線形結合」などの概念だ。東大に合格するような高校生は、すでにこの問題が解けるのだから、そういうところでつまずく心配はないだろう。教える方としても、大きな面倒が省けて非常に嬉しいはず。ちなみに、環とか代数系というのは、量子力学の交換関係に密接な関係があるので、若いうちに一生懸命やっておくのは決して無駄ではない。
(2)は、行列の積がつくる集合の構造のチェックに相当するだろう。「変換」としたいところだが、量子力学の意味で「行列の変換」に対応するのは、演算子の変換であり、それはA'=BAB-1に相当する。この問題では、Bあるいはその逆行列を左から掛けるだけだから、厳密には「変換」とはいえない。が、それに似たような計算で、変換の練習をしていると考えれば、物理を目指す学生は納得できるかもしれない。
数学の観点からすると、AとBの積の結果が、ある集団に対し閉じているかどうか調べよ、というのが(2)の要旨となろう。c=0なので、Aは三角行列という特別な形になる。これは問題を解く上で非常に重要な条件となろう。三角行列の行列式は対角要素の積になる、という有名な関係がある。実際、数値的に大きな次元をもった行列のdetを求めるときは、三角化する方法がよく使われる。ちなみに、この問題では、Aは上三角行列になっている。任意の行列は上三角行列と下三角行列の積に分解できるという定理がある(LU分解)。これも、数値計算で線形代数、ひいては量子力学の研究を行う時の必須アイテムだ。
問題を解くにあたっては、det(A)=ad=±1となったことに注目する。和(差)の演算が消えて、積だけになったのが非常に大きな特徴と捉えるべし。このことから、a,dが特定できるようになったからだ。a,dともに整数という制限があるので、この条件を満たす組み合わせは4つしかない。つまり(a,d)=(+1,+1), (-1,-1)、これはdet(A)=1の場合。そして、(a,d)=(+1,-1), (-1,+1)、これはdet(A)=-1の場合。この4つの場合について、丁寧に調べていけばよい。しかし、bが決まらないので、ここの処理が勝負の分け目となる。
手を動かして計算してみると、BnAもB-nAも、同じような構造になることがわかる。それは
という形にまとめられる。a,d=±1なので、結局、この行列は
と書いてよい。ただし、気をつけるのは符号の使い方で、対角要素の符号は、いわゆる「符号同順」ではない。あらゆる組み合わせ(つまり4通り)を考えてよい。またnの符号もどちらか好きな方を適当にとってよい。nはBあるいはB-1を掛ける回数だから、当然0を含む正の整数(自然数?)。
つまり、BnあるいはB-nは上のような行列の集合を形成する。この集合の中に、問題に示された行列は含まれるかどうか議論すればよい。明らかに、それは
b±n=0が成り立つかどうかにかかっている。b>0ならば、b-nになるような積をn(=b)回繰り返せばよい。一方、b<0ならb+nの場合を選びn(=b)回だけ行列の積を計算するとよい。ちなみに、b=0の場合は積などやらずとも、Aが最初から望みの形になっていることは明らか。bが整数である、という条件がこの問題では効いているのだ。これは、量子力学で、量子数を算出する条件を導出するのと似たような思考法だ。とてもおもしろい問題だと思う。
(3)は、また一般の形式に戻る。BAもB-1Aも、ここでは具体的に計算しないといけない。|X|+|Z|に相当するのは、|a±c|+|c|となる。この先はあまり行列や線形代数とは関係ない展開となるので、なんだこりゃ?と思う人も多いだろう。
基本的には、a>0, c>0の場合の|a-c|+|c|を考えるだけでいいことが、いろいろ分析していくと判明する(残りの3つの場合は、正の数a’>0などを導入し、a=-a'と置き換えてやると、全ての場合が最初の場合と等価であることが示せる)。この証明はあまりにも簡単すぎてここに書く気がしない。多少は三角不等式やSchwarzの不等式などと関係しているかと思ったが、まったくこの問題とは無関係だった。がっくり。この問題の本質はc>0ということだけ。これは、場合分けがあるように見せかけて受験生を脅かし、時間不足にするのが狙いか?と疑ってしまう!この問題の内容は、大学で勉強するためには不要なんじゃないか?
ちなみに、MITの講義では、太陽からの光線がポインティングベクトルになっていることを紹介し、その大きさは1.4kW/m2だといっていた。これがいわゆる太陽定数だ。太陽光発電をする際は、これが発電エネルギーの上限値に相当する。教授の説明では、パネルを砂漠一面に敷き詰めても、全米のエネルギー消費量を賄う量には届かないとか。「太陽光発電っていうのは、そういう意味では残念なエネルギーなんですよ」と解説していた。(調べてみると、実は、彼は核物理出身なのだった...)
この講義によると、アメリカの保有する発電所の出力は7.0E5(MW)、つまり700,000,000kWあるという。太陽定数で割ると、500km2程度になる。仙台市の面積は760km2、横浜市は440km2だというから、発電効率100%だとしたら、仙台と横浜の中間程度のかなり広い土地を太陽パネルで埋め尽くさないとアメリカ一国の発電量を賄えないことになる。実際には、太陽光発電の効率は30%程度らしいから、さらに3倍以上の面積が必要になる。だいたい1700km2と見積もると、大阪の面積がだいたい1900km2だというから、その9割近くをパネルで埋め尽くすことになる。
これはたしかに大変な事業だとは思うが、不可能ではないと思う。アメリカなら、そのくらいの土地なら余っていそうな気もする。MITの教授は太陽光発電を「残念」と評したが、むしろ太陽光発電の方がやりがいのある、チャレンジのしがいのある事業のような気がして来た。
この問題を思えば、昨年の東大の2次試験の数学の方がずっと簡単で、よい問題が含まれていたと思う(全部は見てないので断定はできないが)。例えば、第5問の平行四辺形と一次変換を組み合わせた問題は、大学に入ってから再登場する概念が組み合わされていて、後でとても役に立つと思われる。だから、答えを得るだけではなく、その内容の吟味が大事だろう。もちろん、試験中の学生は正解を得ることだけを考えればよいのだが、日頃の勉強では存分に問題を研究し、その真の意味や背景をえぐり出すよう努力すべきだ。
ちなみに、東大の理系の数学は150分で6問を解く。全問解答を狙うなら、一つ25分ということになるが、昨年の第5問はちょうどそのくらいの時間で解ける。(よく訓練された受験生ならもっと短い時間で解けるだろう。)
さて、この問題から学べることを探してみる。2次元の正方行列。行列要素はすべて整数。たぶん、この「整数」というのが強い条件になるはず。量子力学でも整数は大きな役割を果たす。実数と違って、整数には「隙間」があるからだ。最後に、この行列要素から作ったベクトルがなす平行四辺形の面積は1になるという。実際に問題を解くときは、この条件をどう使うかが問題となろう。
2つのベクトルが成す平行四辺形の面積は、大学では電磁気学でよく取り上げられる。今思いつくのはポインティングベクトル。これは、電磁場によって運ばれるエネルギー流(束)のことで、イメージとしては太陽からやってくるエネルギー、いわゆる「太陽エネルギー」がよい例となろう。youtubeに公開されているMIT物理の講義の一つがまさにポインティングベクトルについてであり、実は太陽エネルギーの例もこの講義の中で取り上げられている。
ポインティングベクトル(S)は、電場ベクトル(E)と磁場ベクトル(B)の外積で表される、つまりS=E×B(比例定数は1に規格化した....)。このエネルギー流の大きさ(たとえば太陽エネルギーの大きさ)を計算するときは、Sの大きさ(ノルム)を計算することになるが、それがまさにEとBがつくる「平行四辺形の面積」の計算に相当している。
電場と磁場の2つのベクトルの外積の結果得られたベクトル(すなわちS)の方向は、この平行四辺形がつくる面に垂直な方向を向いている。このことから、電磁場というのは横波であり、電磁場の揺れる方向に対して垂直方向に電磁波自体は伝搬するという性質がわかる。
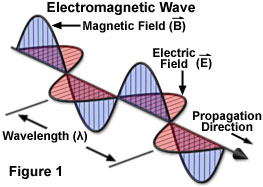 |
| 電磁場の進む方向(Propagation direction)は、 電場(E)や磁場(B)の振動する方向と垂直な方向になっている。 フロリダ州立大のホームページより。 |
回転操作を座標全体に対して行えば(つまり座標軸の回転変換)、特別な状況から一般的な状況にもどることができる。ここで大切なのは、回転操作はベクトル同士が成す角度を不変に保つという性質だ。また、ノルム(つまりベクトルの長さ)も回転操作に対して不変だというのも大事だ。このように、ある座標変換に対して「不変な量」を探し出すのが、量子力学が誕生して以降の物理学の考え方の基本だ。この問題でも、それに似たようなことを「楽しむ」ことはできる。すなわち、x軸を電場に沿って取った特別な座標から、電場が(a,b)、磁場が(c,d)を向いているような一般座標に回転変換したとしよう。この変換をしても角度θとノルム|E|と|B|は不変なんだから、平行四辺形の面積も不変に保たれる(当然といえば当然だが)。この座標において、|E|と|B|は、それぞれ(a,b)と(c,d)を使って表される(ピタゴラスの定理)。また、θに関してはEとBの内積E・Bによって表す事ができる(正確にはcosθの形だが...)。sin2θ+cos2θ=1を使えば、sineとcosの変換は自由にできるから、内積とノルムを使って、どんな座標系でも使える平行四辺形の面積公式を得る事ができる。内積の定義からE・B=|E||B|cosθ。これをsinθに変換し、上で求めた平行四辺形の面積公式、つまりS=|E||B|sinθに代入すると、
題意から、四辺形の面積は1に拘束されているのでS=1であるが、ad-bc=det(A)、つまりAの行列式の値としてはdet(A)=±1ということになる。実はこのようなタイプの行列をユニタリー行列といって、量子力学で最も重要な変換行列として頻繁に登場する。ちなみに、det(A)=1は回転などパリティが変わらないタイプの変換に相当し、det(A)=-1は鏡映反転などパリティが変わるタイプの変換に相当する。同じユニタリー変換といっても、det(A)の符号が異なる変換同士は連続変換によって結びつけることはできない。ちなみに、行列Bのdetは1だから(det(B)=1)、ある種の回転操作と見なすことができる。
(1)では、とりあえず行列の計算はやってみてもよいだろうが、基本的には行列式を中心に考えるのがよい。detの関係式として有名なものに、det(A)det(B)=det(AB) = det(BA)というのがある。この問いではまさにこれを使う。det(B)=1であることはすでに考察済みだから、det(BA)=det(A)となる。|det(A)|=|ad-bc|=1だから、行列BAの行列要素でつくる平行四辺形の面積は、行列Aの要素でつくる平行四辺形の面積と同じ1であることが示された。
同じようにして、B-1B=E、Eは単位行列、に関して行列式を考えると、det(B-1)det(B) = det(E)、Eは単位行列、なので、det(B-1)= 1/ det(B)=1を得る。従って、det(B-1A)=det(A)=±1となり、この行列要素からなる平行四辺形も面積が1のままであることがわかる。
BAやB-1Aの行列要素が整数のままであるのは、行列の積は、行列要素の観点からすると、和と積の2種類の演算の組み合わせ(つまり線形結合)だから、この演算は閉じている(つまり計算の結果が、整数の集合から飛び出さない)ことがわかる。和と積という2種類の演算が定義された集合の事を「環」、あるいは「代数系」というらしい。仮に、行列の積に割算が含まれるようなことになると、整数÷整数は必ずしも整数に戻らないから、演算は閉じず、結果の行列が非整数の行列要素をもってしまうこともあり得る。行列の積は「線形結合」なんですよ!という出題者からのメッセージだと、この問題は受け取るべきだろう。実際、大学に入学して、最初に理系の学生が挫折しかかり、ショックを受けるのが、線形代数の「一次独立」、「線形結合」などの概念だ。東大に合格するような高校生は、すでにこの問題が解けるのだから、そういうところでつまずく心配はないだろう。教える方としても、大きな面倒が省けて非常に嬉しいはず。ちなみに、環とか代数系というのは、量子力学の交換関係に密接な関係があるので、若いうちに一生懸命やっておくのは決して無駄ではない。
(2)は、行列の積がつくる集合の構造のチェックに相当するだろう。「変換」としたいところだが、量子力学の意味で「行列の変換」に対応するのは、演算子の変換であり、それはA'=BAB-1に相当する。この問題では、Bあるいはその逆行列を左から掛けるだけだから、厳密には「変換」とはいえない。が、それに似たような計算で、変換の練習をしていると考えれば、物理を目指す学生は納得できるかもしれない。
数学の観点からすると、AとBの積の結果が、ある集団に対し閉じているかどうか調べよ、というのが(2)の要旨となろう。c=0なので、Aは三角行列という特別な形になる。これは問題を解く上で非常に重要な条件となろう。三角行列の行列式は対角要素の積になる、という有名な関係がある。実際、数値的に大きな次元をもった行列のdetを求めるときは、三角化する方法がよく使われる。ちなみに、この問題では、Aは上三角行列になっている。任意の行列は上三角行列と下三角行列の積に分解できるという定理がある(LU分解)。これも、数値計算で線形代数、ひいては量子力学の研究を行う時の必須アイテムだ。
問題を解くにあたっては、det(A)=ad=±1となったことに注目する。和(差)の演算が消えて、積だけになったのが非常に大きな特徴と捉えるべし。このことから、a,dが特定できるようになったからだ。a,dともに整数という制限があるので、この条件を満たす組み合わせは4つしかない。つまり(a,d)=(+1,+1), (-1,-1)、これはdet(A)=1の場合。そして、(a,d)=(+1,-1), (-1,+1)、これはdet(A)=-1の場合。この4つの場合について、丁寧に調べていけばよい。しかし、bが決まらないので、ここの処理が勝負の分け目となる。
手を動かして計算してみると、BnAもB-nAも、同じような構造になることがわかる。それは
という形にまとめられる。a,d=±1なので、結局、この行列は
つまり、BnあるいはB-nは上のような行列の集合を形成する。この集合の中に、問題に示された行列は含まれるかどうか議論すればよい。明らかに、それは
b±n=0が成り立つかどうかにかかっている。b>0ならば、b-nになるような積をn(=b)回繰り返せばよい。一方、b<0ならb+nの場合を選びn(=b)回だけ行列の積を計算するとよい。ちなみに、b=0の場合は積などやらずとも、Aが最初から望みの形になっていることは明らか。bが整数である、という条件がこの問題では効いているのだ。これは、量子力学で、量子数を算出する条件を導出するのと似たような思考法だ。とてもおもしろい問題だと思う。
(3)は、また一般の形式に戻る。BAもB-1Aも、ここでは具体的に計算しないといけない。|X|+|Z|に相当するのは、|a±c|+|c|となる。この先はあまり行列や線形代数とは関係ない展開となるので、なんだこりゃ?と思う人も多いだろう。
基本的には、a>0, c>0の場合の|a-c|+|c|を考えるだけでいいことが、いろいろ分析していくと判明する(残りの3つの場合は、正の数a’>0などを導入し、a=-a'と置き換えてやると、全ての場合が最初の場合と等価であることが示せる)。この証明はあまりにも簡単すぎてここに書く気がしない。多少は三角不等式やSchwarzの不等式などと関係しているかと思ったが、まったくこの問題とは無関係だった。がっくり。この問題の本質はc>0ということだけ。これは、場合分けがあるように見せかけて受験生を脅かし、時間不足にするのが狙いか?と疑ってしまう!この問題の内容は、大学で勉強するためには不要なんじゃないか?
ちなみに、MITの講義では、太陽からの光線がポインティングベクトルになっていることを紹介し、その大きさは1.4kW/m2だといっていた。これがいわゆる太陽定数だ。太陽光発電をする際は、これが発電エネルギーの上限値に相当する。教授の説明では、パネルを砂漠一面に敷き詰めても、全米のエネルギー消費量を賄う量には届かないとか。「太陽光発電っていうのは、そういう意味では残念なエネルギーなんですよ」と解説していた。(調べてみると、実は、彼は核物理出身なのだった...)
この講義によると、アメリカの保有する発電所の出力は7.0E5(MW)、つまり700,000,000kWあるという。太陽定数で割ると、500km2程度になる。仙台市の面積は760km2、横浜市は440km2だというから、発電効率100%だとしたら、仙台と横浜の中間程度のかなり広い土地を太陽パネルで埋め尽くさないとアメリカ一国の発電量を賄えないことになる。実際には、太陽光発電の効率は30%程度らしいから、さらに3倍以上の面積が必要になる。だいたい1700km2と見積もると、大阪の面積がだいたい1900km2だというから、その9割近くをパネルで埋め尽くすことになる。
これはたしかに大変な事業だとは思うが、不可能ではないと思う。アメリカなら、そのくらいの土地なら余っていそうな気もする。MITの教授は太陽光発電を「残念」と評したが、むしろ太陽光発電の方がやりがいのある、チャレンジのしがいのある事業のような気がして来た。
2013年2月6日水曜日
センター試験:数学IAの第二問の最後の問
さて、この大問の最後は平行移動の問。y=2x2を平行移動して、点(p,q)を通過するようにするには、x → x-p, y → y-qと変換する。
実はこれは物理でいうところの「ガリレオ変換」(あるいは並進移動)に相当する。大学で力学を習えば、「ニュートン方程式はガリレオ変換に不変で、その意味では相対性を持っている。しかし、4次元空間におけるローレンツ変換には不変ではないから、真の意味では相対性理論にはなってない」などといった講義を受けるはずだ。絶対座標の有無や、座標変換の理論を習いながら、慣性や慣性系の意味などを学ぶ。
このような理論や概念の説明に進む前に、計算でつまずかれては、話の腰を折られるようなものだ。この問題を作った先生は、大学一年生に力学を教える時、楽をしたいと思ったのかも。
さらに、非相対論的な量子力学でも並進変換は登場する。ここではハミルトニアンが並進対称性を持っている所から出発して、運動量保存則を導出する。量子状態の並進変換はexp(-iaP/ℏ)というLie群型のユニタリー演算子によって実現される。ここでは、並進距離はaで表され、Pは運動量演算子に対応する。(この表現は1次元だが、運動量演算子の可換性により、容易に三次元の場合へと拡張できる。)具体的には、exp(-iaP/ℏ) H exp(iaP/ℏ) = Hであることを利用して、aに関しての無限小変換に対してTaylor展開を行い、HP-PH=0、すなわち[H,P]=0を導出する流れとなる。(Hはハミルトニアンを表す。)話が飛びすぎてしまったので、この辺りで試験問題に戻ろう。
この問題では、y-q = 2(x-p)2を出発点として、この放物線が、ある瞬間t1において3点O, P, Qを通ることを利用して、t1を計算しようというものだ。あたえられた放物線に沿って「運動」しているP,Qは時間tによってパラメーター表示できるので、それを平行移動した放物線の式のx,yに代入する。また、Oを通ることから、q=-2p2という条件が手に入る。qは負の数であることは明らか。このようにして、3点を通ることから得られる条件式を3つ求め、それを連立して解いて、3つの未定変数p,q,t1を決定するだけ。計算が煩雑になりがちだが、相殺する項をうまく抜き出してやると、上のp、qに関する関係式以外は、t1とpの一次式になることが判明する。この連立方程式を解いて、2つの未定数を決定し、最後にqを計算する。
こういうパラメータ表示は、数値計算などでよく使われる。モデル計算や数値シミュレーションでもよく使う手法だ。大学に入って来た学生がパラメータ表示を使いこなせしてくれたら、すぐに理論の説明に取りかかれるから教えやすいのは明らか。これはよい問題だと思う。
実はこれは物理でいうところの「ガリレオ変換」(あるいは並進移動)に相当する。大学で力学を習えば、「ニュートン方程式はガリレオ変換に不変で、その意味では相対性を持っている。しかし、4次元空間におけるローレンツ変換には不変ではないから、真の意味では相対性理論にはなってない」などといった講義を受けるはずだ。絶対座標の有無や、座標変換の理論を習いながら、慣性や慣性系の意味などを学ぶ。
このような理論や概念の説明に進む前に、計算でつまずかれては、話の腰を折られるようなものだ。この問題を作った先生は、大学一年生に力学を教える時、楽をしたいと思ったのかも。
さらに、非相対論的な量子力学でも並進変換は登場する。ここではハミルトニアンが並進対称性を持っている所から出発して、運動量保存則を導出する。量子状態の並進変換はexp(-iaP/ℏ)というLie群型のユニタリー演算子によって実現される。ここでは、並進距離はaで表され、Pは運動量演算子に対応する。(この表現は1次元だが、運動量演算子の可換性により、容易に三次元の場合へと拡張できる。)具体的には、exp(-iaP/ℏ) H exp(iaP/ℏ) = Hであることを利用して、aに関しての無限小変換に対してTaylor展開を行い、HP-PH=0、すなわち[H,P]=0を導出する流れとなる。(Hはハミルトニアンを表す。)話が飛びすぎてしまったので、この辺りで試験問題に戻ろう。
この問題では、y-q = 2(x-p)2を出発点として、この放物線が、ある瞬間t1において3点O, P, Qを通ることを利用して、t1を計算しようというものだ。あたえられた放物線に沿って「運動」しているP,Qは時間tによってパラメーター表示できるので、それを平行移動した放物線の式のx,yに代入する。また、Oを通ることから、q=-2p2という条件が手に入る。qは負の数であることは明らか。このようにして、3点を通ることから得られる条件式を3つ求め、それを連立して解いて、3つの未定変数p,q,t1を決定するだけ。計算が煩雑になりがちだが、相殺する項をうまく抜き出してやると、上のp、qに関する関係式以外は、t1とpの一次式になることが判明する。この連立方程式を解いて、2つの未定数を決定し、最後にqを計算する。
こういうパラメータ表示は、数値計算などでよく使われる。モデル計算や数値シミュレーションでもよく使う手法だ。大学に入って来た学生がパラメータ表示を使いこなせしてくれたら、すぐに理論の説明に取りかかれるから教えやすいのは明らか。これはよい問題だと思う。
登録:
投稿 (Atom)





